Por Gustavo Niz

Encontremos un buen tono para comenzar a hablar del coronavirus…
“The bad news is that everyone is a potential victim …but the good news is that everyone is a potential solution” (Bobi Wine, https://www.youtube.com/watch?v=PUHrck2g7Ic)
…o quizá podríamos empezar con este otro tono que ha usado el famoso George Weah para compartir entre la población de Liberia las políticas de la sana distancia e higiene (https://www.youtube.com/watch?v=kZm_beXeVzs)
Ahora sí, comencemos…
Lo primero que se aprende al tratar de modelar epidemias es que NO resulta simple hacerlo, pero tampoco imposible e inútil. Son fenómenos que involucran un vasto número de variables biológicas, económicas, sociales, políticas y físicas, por lo que sus simplificaciones matemáticas pueden o no ser suficientemente realistas. A su vez, la predicción del modelo puede influir en la toma de decisiones posteriores, y por ende influir en la epidemia, desviándonos claramente de la predicción original. Sin embargo, estos modelos más que pensados como la verdad absoluta del futuro, proveen de escenarios que cualitativa, e incluso cuantitativamente, nos pueden ayudar a tomar decisiones que, en su momento, consideramos correctas para proteger a las poblaciones expuestas.
No pretendemos ser ambiciosos y describir todos los modelos sobre epidemias que existen, pero sí algunos de los más populares y básicos, que durante el covid-19 han tomado popularidad en comunicados oficiales, redes sociales y algunos artículos científicos. Nuestra descripción puede resumirse en este esquema y que describiremos a lo largo de este ensayo.

Con esta idea de simplificar la realidad en un modelo físico usando matemáticas lo que necesitamos es comprender cuál es la esencia que describe a este sistema. En una primera instancia, podemos pensar que las epidemias se reducen a individuos, idealizados como canicas o pelotitas, que se mueven libremente dentro de un cierto espacio (por ejemplo, una cajita cuadrada en dos dimensiones) y que transmiten al virus sólo por “estar cerca” de otros individuos. Existen varias maneras de mover a las canicas y de las interacciones o “reglas sociales” entre ellas, pero de forma pictórica se reducen al siguiente esquema:

En esta primer fase de simplificación hemos ya descartado muchas variables que pueden resultar importantes en una epidemia real, como el modo exacto de transmisión del virus. Sin embargo, regresaremos a ellas en su momento y veremos cómo incluir algunas. Por ahora, sólo veamos cómo funciona esta primera aproximación de la realidad. Tenemos una caja con canicas azules que están saludables y llega una canica roja contagiada. La canica roja se mueve libremente y con cierta probabilidad de infectar a las otras. Si la probabilidad es suficientemente alta la gente se infecta rápido y los contagiados crecen exponencialmente. Una forma bonita de apreciar este crecimiento de la epidemia es con el número de reproducción [katex] R_{0} [/katex] (“erre cero”), que de forma efectiva nos dice cuántas personas en promedio serán contagiadas por un enfermo durante su periodo infeccioso. Ahora dividamos al tiempo en intervalos regulares ligados a estos contagios; en donde cada intervalo temporal ser de uno o más días. Por ejemplo, si consideramos [katex] R_{0} =2 [/katex] y que contamos con un solo infectado en el primer intervalo temporal, al que llamamos [katex] t_{1} [/katex], entonces para el segundo intervalo de tiempo, [katex] t_{2} [/katex], habrá (1 infectado en [katex] t_{1} [/katex]) [katex] \times R_{0} =2 [/katex] nuevos infectados, o un total de 3 infectados acumulados. Al siguiente tiempo, [katex] t_{3} [/katex], habrá (2 infectados en [katex] t_{2} [/katex]) [katex] \times R_{0} =4 [/katex] nuevos infectados, o un total de 7. Para [katex] t_{4} [/katex] serán 8 nuevos y 15 totales. Noten que los infectados nuevos crecen como 1,2,4,8,16,32,… que es [katex] R_{0} [/katex] elevado al exponente dado por el número de intervalo temporal en el que vamos. Si los intervalos fueran días, para el día 27 tendríamos 227=134,217,728, es decir, algo así como la población de México de nuevos infectados para un [katex] R_{0} =2[/katex].
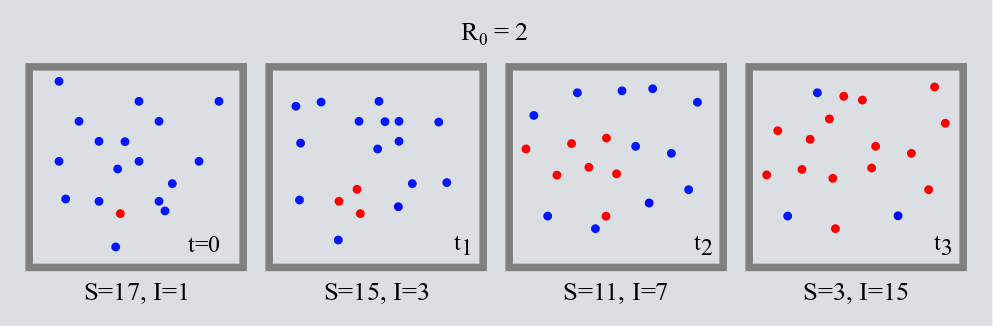
Se cree que para el coronavirus el número de reproducción es de alrededor de [katex] R_{0} =2.2[/katex], donde la parte fraccionaria de 0.2 no corresponde al contagio de casi un cuarto de persona, sino a un promedio estadístico. Por ejemplo, si tenemos a 10 infectados de un virus con [katex] R_{0} =2.2[/katex], ocho de estos diez infectarán a 2 personas cada una y los otros dos restantes a 3 cada una. Es difícil de saber con exactitud el valor de [katex] R_{0} [/katex] para el coronavirus pues no se cuentan con experimentos de contagio libres, esto es, sin intervenciones sobre la epidemia, y que sean lo suficientemente grandes como para tener una buena estadística. Afortunadamente, con los datos que tenemos sabemos que el coronavirus no parece ser tan infeccioso como la varicela o el sarampión, los cuales tienen un [katex] R_{0} [/katex] del orden o mayor a 10 respectivamente.
Regresemos a nuestro modelito de juguete; conforme se infectan las canicas azules (Susceptibles) por las canicas rojas (Infectados) a un ritmo exponencial dado por [katex] R_{0} [/katex], llega un momento en que ya no hay tantas canicas azules que puedan ser infectadas y la tasa de infección baja, es decir, se satura la población de infectados nuevos y después empieza a declinar hasta que alcanzan cero, pues ya se ha infectado a toda la población. Si sólo observamos a los infectados acumulados tenemos una curva que comienza lento, después crece exponencialmente, pero llega un momento en el que se satura.
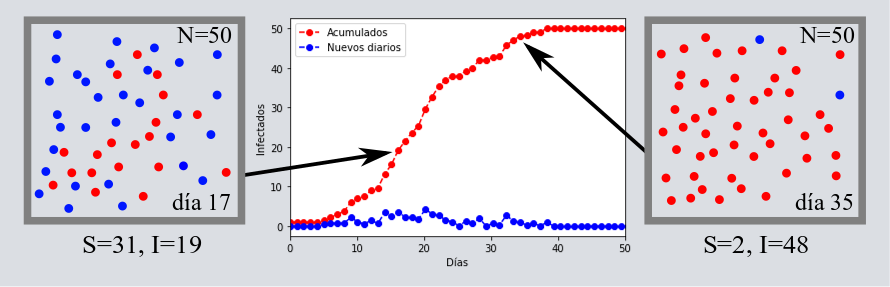
Observemos que una forma de mitigar o desacelerar la pandemia es reduciendo este número [katex] R_{0} [/katex] desde el principio, o en cualquier momento de la epidemia. Esto se puede lograr con mecanismos que disminuyan la probabilidad de contagio, que pueden ser de carácter físico como la sana distancia, el usar cubrebocas, visores, guantes, etc., pero también los hay a un nivel bioquímico o más fundamental, como por ejemplo, procurando un sistema inmunológico más fuerte de los individuos susceptibles, y de ahí la sugerencia de dormir las horas necesarias, evitar estrés, comer saludable, hacer ejercicio, etc. A su vez, noten que si este número de reproducción efectivo es menor a uno, es decir, si cada persona infecta a menos de un individuo en promedio, entonces la epidemia se detiene, como mostramos en la siguiente imagen.
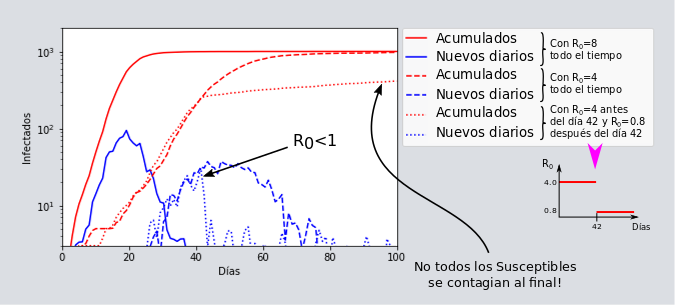
Otra forma alternativa de mitigar la epidemia es reduciendo al número de susceptibles, ya sea desde el principio o a lo largo de brote epidémico. Un ejemplo de este control es un “lockdown” fuerte, donde los individuos dejan de tener cualquier contacto entre sí, y por ende ya no son susceptibles a ser infectados. Reducir el [katex] R_{0} [/katex] o el número de susceptibles es de alguna manera equivalente, y por eso nos concentraremos en llamarlo [katex] R_{0} [/katex] efectivo.
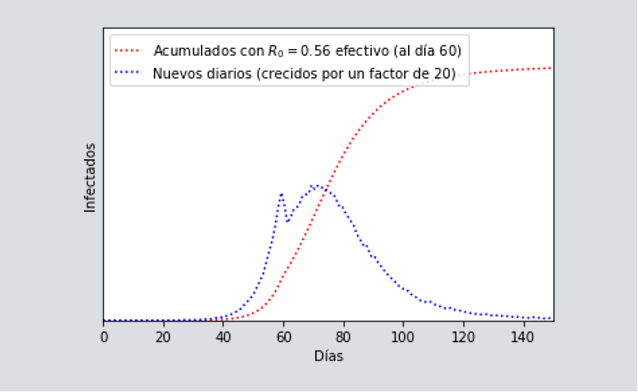
En el caso de aplicar el “martillo” (como lo llama Tomas Pueyo), y que se resume en detener fuertemente la pandemia y no sólo aplanar la curva. Esto es lo que han logrado la mayoría de los países que han culminado con esta primera ola de infección, y cuyos detalles particulares discutiremos más adelante. En este caso, pueden ocurrir varias cosas dependiendo de qué tan por debajo de 1 es el [katex] R_{0} [/katex] efectivo. En el caso de un [katex] R_{0} [/katex] cercano a 1, entonces la epidemia puede terminar abruptamente, o bien quedarse por un tiempo ya sea en un máximo muy largo (incluso de varias semanas y como parece ocurrir con Canadá), o bien, subir y bajar varias veces (con varios máximos) hasta que decide descender completamente. Aquí un ejemplo de ello donde se observan dos máximos, con el segundo más largo que el primero.
Introduzcamos un ingrediente más en nuestro modelo y, ahora, pensemos que después de un cierto número de días las canicas rojas se curan o se mueren, volviéndose de color verde (Removidos = recuperados + muertos). Como resultado, tenemos tres curvas: los Susceptibles ([katex] S[/katex]) que disminuye en el tiempo hasta llegar a cero, los removidos ([katex] R[/katex]) que crece hasta el total de la población de canicas, y los infectados ([katex] I[/katex]), que después de saturarse comienzan a decrecer hasta llegar a cero. Esta última es la famosa curva de los infectados que tiene forma de campana, y que hemos visto por muchos lados bajo el slogan de “aplana la curva”. Aquí un ejemplo de cómo se vería la evolución de un modelo con estos tres grupos, [katex] S[/katex], [katex] I[/katex] y [katex] R[/katex].
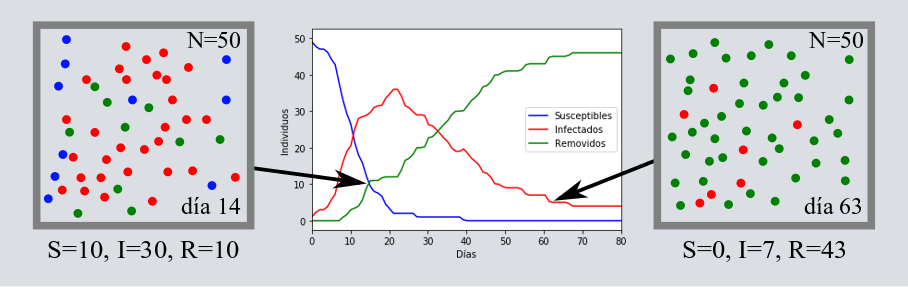
Para una discusión más detallada sobre el modelaje que hemos hecho de este tipo te invitamos a leer “Usando Pelotitas para Entender al Covid-19” (próximamente).
Pues bien, podemos hacer una infinidad de simulaciones de canicas rojas, azules y verdes para entender de qué forma las epidemias avanzan, ajustándose decentemente a mucho ejemplos que hay en la historia (como el épico caso de la gripe Española de 1918). A su vez, para ser más realistas podemos introducir más ideas en el juego de las canicas. Por ejemplo, podemos introducir super-canicas (que serían superportadores del virus), canicas que dejan de moverse o infectar (cuarentena), canicas que dejan de moverse (muertos), diferentes geometrías donde se puedan mover los individuos o espacios físicos con regulaciones particulares donde puedan o no entrar las canicas rojas, etc. A todos estos modelos se les llama de agentes. Sin embargo, podemos movernos nuevamente en el sentido opuesto y simplificar aún más el modelado. Para ello pensemos en que nos dejan de interesar los individuos per sé, y más bien nos concentramos en la población a la que pertenecen. Entonces, ahora más que canicas azules, rojas y verdes, pensemos en la población de los Susceptibles ([katex] S[/katex]), los Infectados ([katex] I[/katex]) y los Removidos ([katex] R[/katex]). Estos son los llamados modelos de compartimientos epidemiológicos, y uno de los más sencillos de comprender para esta epidemia es el SIR, aunque se utilizan algunas extensiones más complicadas para un modelado más preciso. En el caso del SIR, sólo tenemos que entender las relaciones de cambio entre cada población dependiendo de las otras entre un día y otro. Por un lado, asumimos que la población total no cambia, es decir que [katex] S+I+R[/katex] es una constante que permanece constante en el tiempo, e igual a la población inicial susceptible a contraer la enfermedad. Como consecuencia nos podemos concentrar en[katex] I[/katex] y [katex] R[/katex], pues [katex] S[/katex] será el total de la población susceptible inicial, [katex] N[/katex], menos los infectados y menos los recuperados ([katex] S=N-I-R[/katex]). El cambio en [katex] I[/katex] entre dos días contiguos será por dos vías; por un lado, nuevos infectados aparecen de los susceptibles que fueron contagiados y por otro los que se van a removidos. Como vimos antes existe una probabilidad de contagio que parece inherente al virus, y otra más que depende de cuantos susceptibles haya. Esto lo podemos escribir matemáticamente como que al tiempo [katex] t_{n+1}[/katex], los infectados son los que había el día anterior más un término que depende de los susceptibles y de las propiedades del virus, esto es, [katex] I_{n+1}=I_{n}+\beta (S_{n}/N) I_{n}[/katex]. El factor [katex] \beta[/katex] es constante y nos habla de esta propiedad de contagio inherente al virus y para que sea un probabilidad debe de ser positivo y menor a 1, mientras que el factor [katex] S_{n}/N[/katex] nos habla de la proporción de susceptibles que todavía queda sin infectar en la población al tiempo [katex] t_{n} [/katex]. Nótese que hacia el final de la epidemia, [katex] S[/katex] es casi cero y este factor [katex] S/N[/katex] es pequeño por lo que casi no hay nuevos infectados, como lo discutimos antes. Esta es la curva que siempre crece y que se satura cuando ya no hay susceptibles, y que corresponde al modelo únicamente con canicas azules y rojas. Sin embargo, al introducir a los Removidos (canicas verdes), sabemos que después de un tiempo, los infectados dejan de serlo y pasan a ser removidos. Cuántos removidos nuevos tenemos depende de nuevo de los infectados que tenemos multiplicados por una constante, a la que llamamos [katex] \gamma[/katex], y que nos habla de los días en promedio que un infectado pasa antes de recuperarse o morir. Para el covid, [katex]\gamma[/katex] es como de 0.05 /días, que corresponde a 20 ([katex] = 1 / \gamma [/katex]) días entre ser infectado y pasar a removido. Este número, sobre todo, proviene de la gente que se recupera, pues los muertos son mucho menos en número. Con resto, los removidos al tiempo [katex] t_{n+1} [/katex] son [katex]R_{n+1} = R_{n}+ \gamma I_{n}[/katex]. Como los nuevos removidos eran antes infectados, sabemos que este mismo número desapareció de los infectados, por lo que tenemos que restarle la misma cantidad a la ecuación del cambio en los infectados. De esta manera llegamos a las ecuaciones completas:

Noten que hemos incluido la ecuación de los Susceptibles, pero como ya mencionamos, esta no es nueva y puede deducirse de las otras dos poblaciones, [katex] I[/katex] y [katex] R[/katex]. Si hacemos los intervalos de tiempo super pequeños en lugar de días, las expresiones adoptan naturalmente la forma de derivadas para expresar cambios, y este sistema de ecuaciones se convierte en las llamadas ecuaciones diferenciales del modelo SIR. La solución a este sistema de ecuaciones, nos provee de un promedio suave de las simulaciones con canicas, es decir, de curvas que no brincan tanto como las de arriba. Veamos un ejemplo parecido al de arriba pero ahora con el modelo SIR.
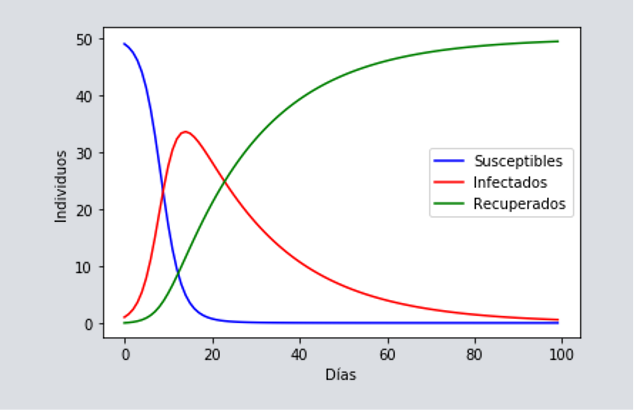
Este sistema de ecuaciones ha sido presentado por muchas personas alrededor del mundo para describir la evolución de la epidemia del Covid. Sin embargo, para ser más realistas se han incluido muchos más compartimientos, que incluyen diferentes grupos de edad, aislamientos, hospitalizados, expuestos al contagio, muertes, vacunas, etc. Un ejemplo con este modelado es el utilizado por el Gobierno de la CDMX, y que encontramos en ModeloCdMx. Además de jugar con el número de poblaciones y cómo se relacionan entre ellas, uno puede imaginar otro tipo de modificación, en la que los parámetros que determinan la probabilidad de moverse de una población a otra (como la [katex] \beta[/katex] y la [katex] \gamma[/katex] que introducimos antes), deja de ser un número constante y ahora es una variable que cambia en el tiempo. ¿Por qué querríamos introducir este cambio? Sabemos que las políticas de intervención varían a lo largo de la epidemia y son estos parámetros ([katex] \beta[/katex] en el caso del SIR) que pueden describir como evolucionan. Para ver detalles sobre estas [katex] \beta[/katex] variables te invitamos a ver “Determinando R0 para el Covid” (próximamente). Con estas herramientas, existen mil y un estudios que uno puede hacer para pensar en entender la pandemia, así como para predecir situaciones futuros.
Si deseas entender con más profundidad, o ver algunas de los estudios que hemos hecho, visita “Jugando con la nobleza del SIR en el Covid-19” (próximamente).
Sin embargo, sabemos que los datos reales son más parecidos a los modelos de agentes (esos de las canicas como individuos), por lo que esperaríamos ver más brincos en estas curvas debido a las mil y un fluctuaciones que provienen de estas variables que hemos omitido. Por ejemplo, una reunión masiva de un grupo particular (como el brote por el grupo Cristiano en el Corea del Sur o alguno de los muchos festivales de música que hubo en el mundo) puede conllevar un brote local importante, que se refleja en un brinco de los infectados para un tiempo particular. Para tratar de modelar este comportamiento menos predecible de los humanos y sus relaciones, uno pueda dar un paso atrás en estos modelos de compartimientos y promover los parámetros a números aleatorios que toman valores dentro algún margen de probabilidad. Estos objetos matemáticos que nos dicen cómo será la probabilidad como función de alguna variable, los llamamos distribuciones de probabilidad, y hay de varios tipos, dependiendo del tipo de dato o información que queremos modelar. Un caso particular es la distribución binomial, que tiene dos (de ahí el nombre de “bi”) posibles salidas; por ejemplo, águila o sol, en el caso de tirar monedas, u obtener un positivo o negativo para el caso de un test PCR de Covid-19. En el caso de promover a [katex] \beta[/katex] y [katex] \gamma[/katex] para el modelo SIR a distribuciones binomiales, uno recupera un comportamiento con brincos más parecidos al modelaje por canicas, y es esta clase de modelos que han resultado más exitosos para describir epidemias, aunque con un mayor grado de incertidumbre.
También hemos jugado con estos modelos, llamados estocásticos, y te invitamos a ver lo que hemos hecho en “Modelos estocásticos de compartimentos para el Covid-19” (próximamente).
Si volvemos a tomar aquella dirección de simplificar aún más el modelo, podemos avanzar un paso adicional. En lugar de pensar en poblaciones o compartimientos que se hablan unas a otras mediante ecuaciones, la última descripción está basada en la curva que sigue de forma efectiva las poblaciones en esta epidemia. En particular para los Infectados acumulados cuando no hay Removidos, la curva se satura como habíamos discutido, y tiene una forma de una “S” acostada (como en la la siguiente figura). A esta curva se le llama logística, y es parte de la familia de las curvas sigmoides, que recientemente han cobrado mucha popularidad por las Redes Neuronales dentro de llamado Aprendizaje Profundo, pero que también es utilizada en medicina, química, física, ciencia de materiales, procesamiento de señales, agricultura, economía, etc. En el caso de epidemias, la curva logística es una solución formal y sencilla de las llamadas ecuaciones de SIS (Susceptible-Infectado-Susceptible, otro modelo de compartimientos), aunque también de otros modelos de compartimientos como el SIR, o sus extensiones más complejas. Por ejemplo, si consideramos a los recuperados o a los muertos por separados, ambas poblaciones siguen la misma curva logística de forma efectiva para epidemias descritas por el modelo SIR, aunque cada una de estas curvas logísticas tiene diferentes parámetros. Una serie de datos que, adicionalmente, sigue esta trayectoria de curva logística es la población de los casos confirmados mediante el test (o algún otro sistema de confirmación clínica) de la enfermedad. Estos casos confirmados corresponden a los Infectados más los Removidos ([katex] I[/katex]+[katex] R[/katex]) dentro del SIR, excepto por un factor que nos dice qué tan bien estamos muestreando a la epidemia con los tests. Este factor puede o no ser constante en el tiempo, y en la mayoría de los casos no corresponde 1, que representa un muestreo del 100% de los casos reales.
La forma explícita de la curva logística está dada por la fórmula en la siguiente imagen y describe esta “S” acostada de la que habíamos hablado como se puede observar. Esta curva está caracterizada por los, parámetros [katex] L[/katex], [katex] t_0[/katex] y [katex] k[/katex] representan, respectivamente, el valor final, el punto de inflexión y la tasa de cambio exponencial inicial. El valor máximo que alcanza la curva, [katex] L[/katex], corresponde a valor al que llegará la epidemia, por ejemplo, el número total de muertos después de una primer ola. El valor de [katex] t_0[/katex], el punto de inflexión, es donde se “dobla” la curva logística y que corresponde al máximo en la curva de casos diarios como se ve en la imagen. Finalmente, el valor de [katex] k[/katex] nos indica con qué coeficiente crecía exponencialmente la epidemia en sus inicios.
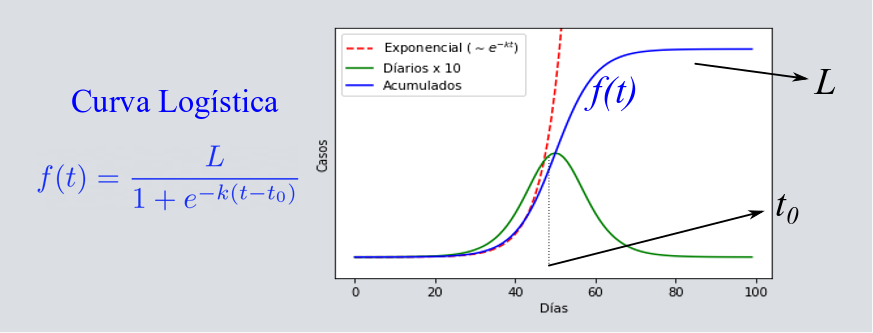
La curva logística no es la única curva que podemos usar para describir de forma efectiva a las epidemias. Existen también las curvas de Hill, Gompertz, Richards (este último una logística generalizada), etc. pero nos concentramos en la logística por su sencilla relación con los modelos de compartimentos, porque tienen pocos parámetros y porque describe la duración completa de epidemias “sencillas”, en contraste con las populares curvas exponenciales que sólo modelan la fase de crecimiento inicial.
Esta última simplificación de una epidemia basada en la curva logística tiene sus pros y contras. Describamos algunos de ellos. Por un lado, es fácil de contrastar con los datos y eficientemente uno puede ajustar los parámetros para realizar predicciones. Además, este modelado no depende fuertemente de las primeras observaciones en las epidemias, que suelen ser datos muy inestables por diferentes factores en su tratamiento, así como por no representar una muestra suficientemente amplia, en el sentido estadístico, de la epidemia. Es por este grado de desconfianza que la mayoría de los trabajos asumen sus primeros datos cuando los casos confirmados han alcanzado al menos 100 individuos. Por el lado de los contras, podemos mencionar que la curva logística es una curva “optimista”, como diría un buen colega, el Dr. Luis Ureña. Esto es debido a que le gusta darse vuelta muy rápido. En términos más precisos, para el día X cuando la epidemia muestra que ha deja el crecimiento exponencial inicial pero que todavía no ha querido reducir el número de casos confirmados diarios, la curva logística que mejor ajusta a los datos es aquella que pocos días después se tuerce o tiene su punto de inflexión. Conforme nuevos datos llegan después de este día X esta curva tiende a subir y subir, hasta que alcanzamos ahora si un punto cercano al de inflexión, y entonces la curva logística que mejor ajusta baja y termina por darnos el resultado correcto (nos referimos a “correcto” en el sentido de que para epidemias que ya terminaron, ésta es la curva final que mejor ajusta los datos). Por consiguiente, son siempre los puntos cercanos al punto de inflexión de la curva (o máximo en los conteos diarios) los que determinan el final la forma exacta de [katex] L[/katex] y [katex] t_0[/katex], que son los críticos para hablar de tasas de mortalidad y otras predicciones que nos gustaría conocer. Otra característica de la curva logística y que también aplica a otras curvas, es que por el grado de simplificación no pueden describir adecuadamente epidemias que cambian mucho en el tiempo, lo que ha ocurrido con muchos casos durante la epidemia que estamos viviendo. Aun así es importante ver que con este grado de simpleza uno puede modelar muchos países correctamente e inferir datos interesantes para el caso de México. Para ver el trabajo que hemos hecho en esta dirección, se invita a consultar otro trabajo más de la serie, titulado “Modelando al Covid-19 con la curva logística” (próximamente).
Finalmente, y antes de terminar con este ensayo, tenemos que hablar sobre la comparación de los datos con nuestros modelos matemáticos. Es un tema que, en principio, merece un tratado aparte, y para ellos hemos preparado esta discusión “Datos y modelos del Covid-19: la discordia”. Sin embargo, a manera de resumen, aquí podemos decir que lo importante es mencionar que no es trivial confrontar estos modelos con los datos. Existen varias razones que complican dicha tarea: en primer lugar, todas las epidemias representan un reto para las sociedades y los sistemas de salud, por lo que muy frecuentemente las series de tiempo de casos confirmados, recuperados, muertes, etc. tienen deficiencias, cambios en definición, retrasos e, incluso, errores en su captura. A su vez, es factible que los responsables no ofrezcan información adicional o definiciones exactas de lo que reportan, o bien, no dispongan de todas las variables necesarias para un análisis completo con estos modelos. Aunado a esta problemática, muchas de las fuentes de información no son de fácil acceso o públicas, imposibilitando parte del debate científico. Muchos de estos sesgos pueden corregirse utilizando el teorema de Bayes, y para no alargar más este, de por sí largo tratado, los remitimos a “Covid-19: Datos y Certidumbre”. Por último, y quizá el punto más importante sobre usar datos de epidemias, es que muchas de las series de tiempo reportadas sólo representan una muestra de la realidad. En el mejor de los casos esta muestra es representativa de la epidemia, pero siempre puede haber sesgos importantes que comienzan a notarse días después, despertando a otros monstruos que no vimos a tiempo…
Los invitamos a descubrir más ideas matemáticas relacionada con el Covid en nuestro Laboratorio de Datos (DataLab de la Universidad de Guanajuato). Estos escritos irán apareciendo conforme nuestros pequeños en casa nos den un poco de tiempo….
“Covid-19: Datos y Certidumbre” por Alma González y Luis Ureña
“Modelos SIR modificados para la evolución del COVID19” (arXiv:004.11352) por Nana Cabo y Alejandro Cabo Montes de Oca
“Aplanar la curva o usar el martillo” por todo el grupo
Usando Pelotitas para Entender al Covid-19 (próximamente)
Modelos estocásticos de compartimentos para el Covid-19 (próximamente)
Jugando con la nobleza del SIR en el Covid-19 (próximamente)
Determinando R0 para el Covid (próximamente)
Modelando al Covid-19 con la curva logística (próximamente)
Datos y modelos del Covid-19: la discordia (próximamente)
El caso de los muertos Corona y su relación con los asintomáticos (próximamente)
Reporte de la pandemia en Guanajuato y México (próximamente)
El equipo de la DCI-Universidad de Guanajuato que trata de entender al Covid-19 usando modelos matemáticos está formado por: Argelia, Alma, Damián, Gustavo, Juan, Miguel, Nana, Luis y Ramón. Más información sobre los integrantes en www.fisica.ugto.mx/~gfm/ y www.fisica.ugto.mx/~datalab/
